What is meant by the Standard Deviation?
Standard deviation denotes the deviation of a set of variables from the mean value. It is the method to determine the reliability of concrete compressive strength results of a batch concrete.
In the design mix of concrete, the target strength should be equal to the characteristic strength plus 1.65 times the standard deviation.
Why is it required for a concrete design mix?
The concrete was produced from a certain mixture of different material and those all are having different properties.
In the design mix, the concrete was calculated by weight method so mistakes may happen. If so standard deviation value was added in concrete design mix for safer side.
Standard Deviation Formula
As per IS 456 follow the below rule to calculate the standard deviation of concrete cubes.
- Rule 1: The standard deviation should be calculated separately for each grade of concrete.
- Rule 2: For the first time, the total number of concrete cube samples should not less than 30 to calculate the deviation.
- Rule 3: The standard deviation value should be calculated separately when significant changes are made in the production of concrete batches.
- Rule 4: The calculation of standard deviation shall be brought up to date after every change of mix design.
| Sample No | Crushing Value in N/Sqmm (X) | Average Strength (M) | Deviation X-M | (X-M)2 |
| 1 | 20 | 24.8 | -4.8 | 23.04 |
| 2 | 20 | 24.8 | -4.8 | 23.04 |
| 3 | 25 | 24.8 | 0.2 | 0.04 |
| 4 | 26 | 24.8 | 1.2 | 1.44 |
| 5 | 27 | 24.8 | 2.2 | 4.84 |
| 6 | 28 | 24.8 | 3.2 | 10.24 |
| 7 | 29 | 24.8 | 4.2 | 17.64 |
| 8 | 29 | 24.8 | 4.2 | 17.64 |
| 9 | 30 | 24.8 | 5.2 | 27.04 |
| 10 | 20 | 24.8 | -4.8 | 23.04 |
| 11 | 25 | 24.8 | 0.2 | 0.04 |
| 12 | 23 | 24.8 | -1.8 | 3.24 |
| 13 | 22 | 24.8 | -2.8 | 7.84 |
| 14 | 21 | 24.8 | -3.8 | 14.44 |
| 15 | 23 | 24.8 | -1.8 | 3.24 |
| 16 | 24 | 24.8 | -0.8 | 0.64 |
| 17 | 25 | 24.8 | 0.2 | 0.04 |
| 18 | 24 | 24.8 | -0.8 | 0.64 |
| 19 | 28 | 24.8 | 3.2 | 10.24 |
| 20 | 26 | 24.8 | 1.2 | 1.44 |
| 21 | 26 | 24.8 | 1.2 | 1.44 |
| 22 | 27 | 24.8 | 2.2 | 4.84 |
| 23 | 21 | 24.8 | -3.8 | 14.44 |
| 24 | 22 | 24.8 | -2.8 | 7.84 |
| 25 | 23 | 24.8 | -1.8 | 3.24 |
| 26 | 24 | 24.8 | -0.8 | 0.64 |
| 27 | 29 | 24.8 | 4.2 | 17.64 |
| 28 | 30 | 24.8 | 5.2 | 27.04 |
| 29 | 22 | 24.8 | -2.8 | 7.84 |
| 30 | 25 | 24.8 | 0.2 | 0.04 |
| Total | 744 | Total | 274.8 |
Example Calculation
Average Strength μ = 744/30 = 24.8 N/Sqmm
n = Number of sample
Std Deviation = √[274.8 (n-1)] = √(274.8/29) = 3.07 N/sqmm
Hence the Standard Deviation of above concrete cube test results – 3.07 N/Sqmm.
As per IS 456, the assumed standard deviation value has mentioned from past records for a similar grade of concrete.
| Grade of Concrete | Assumed Std Deviation (N/Sq.mm) |
| M10 | 3.5 |
| M15 | 3.5 |
| M20 | 4 |
| M25 | 4 |
| M30 | 5 |
| M35 | 5 |
| M40 | 5 |
| M45 | 5 |
| M50 | 5 |
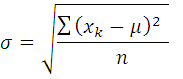
5 Comments
WHAT HAPPENS IF STANDARD DEVIATION FOR M50 IS MORE THAN 5 AND HOW WE CAN RECTIFY THE ISSUE AND WHAT IS THE SOLUTION?
the SD for M50 concrete being greater than 5MPa is not in itself a matter of very serious concern. the value of 5MPA for M50 grade concrete is assumed for design purpose for assuming the Target strength =1.65 *Characteristic strength ie the strength assumed for structural design purpose. the value 5 is used for initial estimation purpose in the absence of actual test results, and hence is on the conservative size, and hence exceeding 5 indicates something amiss in the quality control . with a standard deviation >5 a Larger target strength has to be aimed for so that the probability of any sample being lower in strength than the Characteristic strength is statistically insignificant. however to address the specific question , a better control on the quantities of the inputs, as also uniformity in their quality would help in the matter.
I am interested this work ,generally good jobs
Dear SIR
03 CUBES RESULTS ARE 32,42 & 28 N/mm2
Pl. me know how to calculate individual + or- 15% strength
pl.give me calculation of each cube.
Regards
Hemant Mahukar
if u have 1 sample then u add fck+/4
avg of 3 cube like 25 26 28 Grade-25
25+26+28=77/3=25.66
that’s mean ur cube is pass.