How to Calculate Land Area or Plot Area?

Surveying is an essential preliminary step for any construction work.

The whole site plan determines the structure of a building or a site. We have numerous methods of surveying to understand the nature of a plot.

• Chain Surveying
• Plane Table Surveying
• Compass Surveying
• Topographic Surveying etc

All it does is recording the actual measurements into a paper for easy calculation of area. But how to calculate the plot area? 

How to Calculate Plot Area?

The area is nothing but a space occupied by any geometric shape. For basic area calculations, we could use the below formulas.

But in practical terms, most of the plot do not fall under these geometric shapes. Most common types of plot areas are 

• Triangular Plot
• Irregular Polygons
• Square or Rectangular

To illustrate the formulas, assuming we have different shapes of plots.

Triangle plot

Assuming we have a triangle of 40 feet base & width.

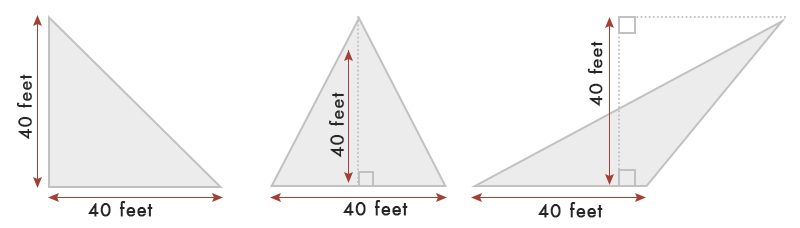
As per the table, Area of triangle = ½ x base x width = ½ x 40 x 40 = 80 Sq.ft

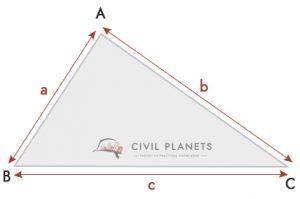
If you can’t be able to measure the height of the triangle and if it is not a right angle, then you could use the below formula

Where S = Perimeter of triangle = (a + b + c)/2

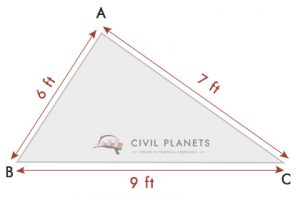
From the drawing, a = 6 feet, b = 9 feet & c = 7 feet, S = (6+9+7)/2 = 11

Therefore, Area of the plot = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 Sq.ft

Irregular Polygons

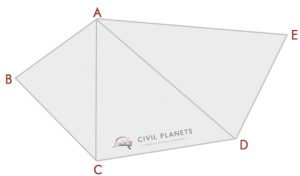
Most of us could recognize this kind of plot. To find the area of this shape, we have to use trigonometry calculation. It’s not that hard.

Let’s find the area of this shape in two typical cases

• Irregular Polygons (with known intersection dimensions)
• Irregular Polygons (with angles)

Irregular Polygons (with known intersection dimensions)

Imagine we have the following plot, with known intersection dimensions.

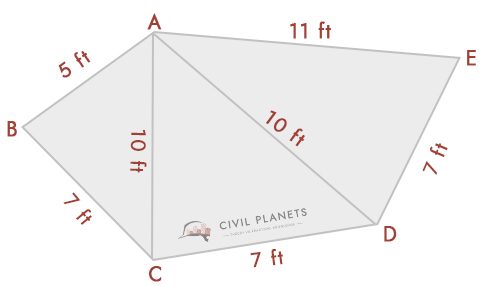
Using the above triangular formula, we can solve this. From the diagram, we have three triangles namely ABC, ACD, & ADE

• Triangle 1 – Δ ABC, Where S = (5+7+10)/2 = 11

Formula for Area = √S(S-a)(S-b)(S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft

• Triangle 2 – Δ ACD, Where S = (10+7+10)/2 = 13.5

Formula for Area = √S(S-a)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft

• Triangle 3 – Δ ADE, Where S = (10+7+11)/2 = 14

Formula for Area = √S(S-a)(S-b)(S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft

So total area of the shape = 16.25+32.79+34.29 = 83.33 Sq.ft

Irregular Polygons (with angles)

Assuming now we don’t know the intersection measurement only having angles like below pic

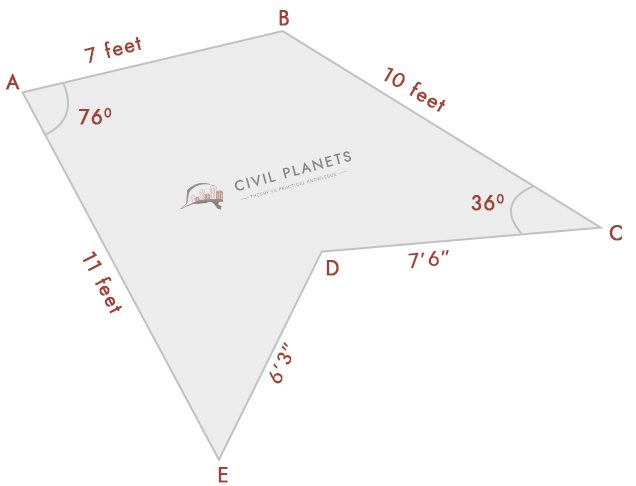
Now separate the above image into three triangles as below

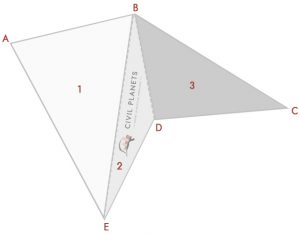
Now we have 3 triangles just like the above, only thing instead of the intersection dimension; we have angles. So the first thing is we have to calculate the intersection measurement using trigonometry.

The intersection measurement can be obtained by Heron’s formula c² = a² + b² – 2abCos(C)

Where, a = length of AB, b = length of AE, c = length of EB

Length of EB = √(a² + b² – 2abCos(C))

= √(7² + 11² – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 feet

Length of DB = √(a² + b² – 2abCos(C))

= √(10² + 7.5² – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 feet

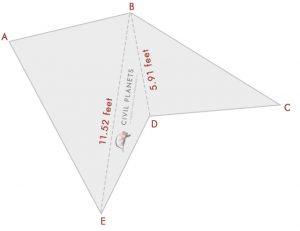
Now we know the length of every side, using the triangle formula, we can calculate the area now

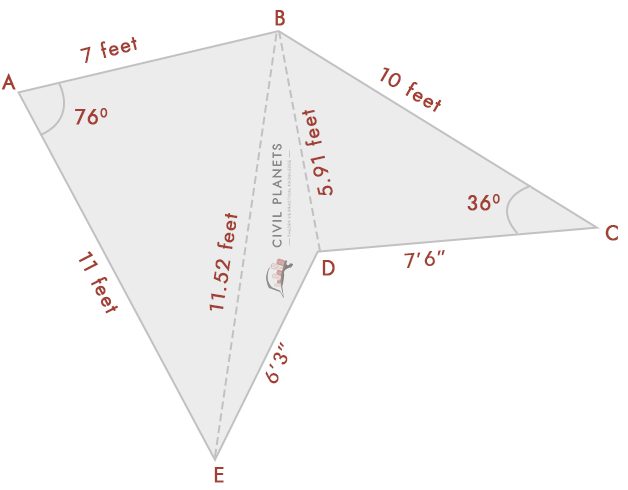
From the diagram, we have three triangles

Triangle 1 – Δ ABE, Where S = (7+11+11.52)/2 = 14.76

Formula for Area = √S(S-a)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft

Triangle 2 – Δ BED, Where S = (11.52+6.25+5.91)/2 = 11.84

Formula for Area = √S(S-a)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft

Triangle 3 – Δ BDC, Where S = (5.91+7.5+10)/2 = 11.70

Formula for Area = √S(S-a)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft

So total area of the shape = 37.35+11.21+21.99 = 70.55 Sq.ft

Happy Learning 🙂