We have discussed Bar Bending Schedule for different structural members such as
Here we are going to discuss the Bar Bending Schedule for Circular Slab
Circular Slab
Circular slabs are not usually common like flat rectangular slabs that we use almost every floor. Circular slabs are used in the following areas
- Water tank cover
- Manhole covers
- A room specifically designed for circular slab
- Towers
- Pump houses constructed above tube wells
- Soak Pit Design
Unlike one way slabs, circular slabs are subjected to bending moments in both directions.
Let’s discuss with an example calculation. Note here we are dealing with a simple manhole cover for calculation purposes; we have taken greater value as the diameter of the slab.
In practice, the circular slab of 3m diameter may have detailed reinforcement.
Circular Slab Reinforcement Detailing
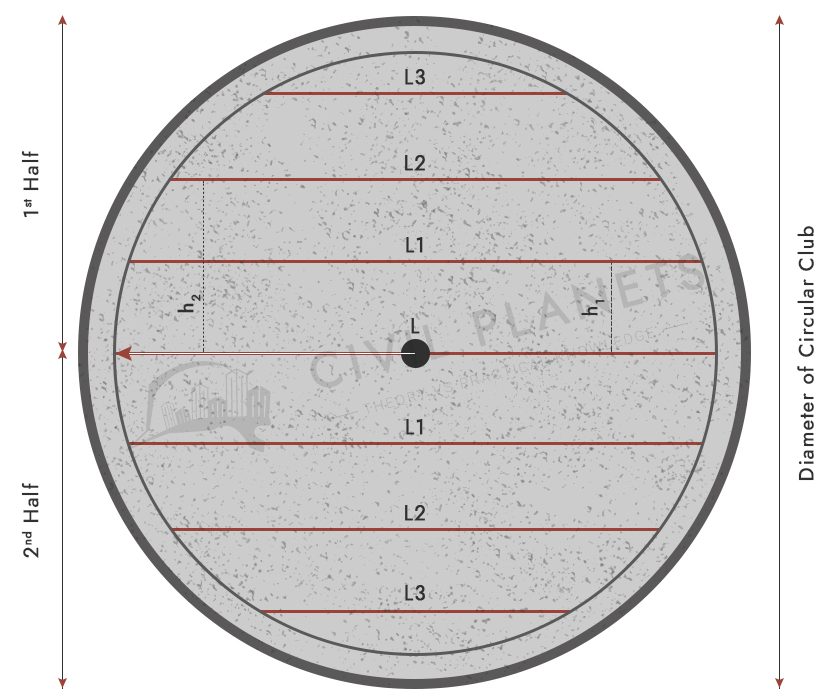
Circular Slab Reinforcement Calculation
Assume you have to prepare a bar bending schedule for a circular slab of 3 metre diameter with 12mm main & distribution bars with 200mm spacing; concrete cover of 25mm.
Splitting the slab into two parts for easy calculation.
Step 1 – Find the Value of L
The only formula you need to remember for the entire calculation is
L = √(R2 – h2) x 2 where
L = Length of the reinforcement
R – Radius of the slab
h – Distance between the reinforcement
From the above diagram, We can calculate the value of L
L = Diameter of Circular Slab – Concrete Cover on both sides = 3000-(2*25) = 2950 mm or 2.95 m
Radius of the slab = (Diameter of the slab – concrete cover on both sides ) / 2 = 2950/2 = 1475 mm or 1.475m
Step 2 – Find the Number of (L) Bars required
Number of L Bars = (Diameter of the slab – concrete cover on both sides)/Spacing = 1475/200 = 7.375 or 7 Nos
Apart from the Centre Rod (L), we need 3 more bars on both sides such as L1, L2, L3
Step 3 – Find the Consecutive Bar Length
For L = √(R2 – h12) x 2 where h1 = distance between L & L1 or spacing of bars – 200 mm
Therefore, L1 = √(R2 – h12) x 2 = √((1475)2 – (200)2)x2 = 2066.7 mm
L2 = √(R2 – h22) x 2= √((1475)2 – (400)2) x 2 = 2007.8 mm
L3 = √(R2 – h32) x 2= √((1475)2 – (600)2) x 2 = 1905.58 mm
Note – The circular slab has reinforcement on both sides, so the value will be multiplied by 2 to get the reinforcement length on the perpendicular side.
Step 4 – Bar Bending Schedule Format – Circular Slab
| Description | Dia of bar (mm) | Number of Bars | Cutting Length (m) | Total Cutting Length (m) | Weight Per Metre (Kg/m) | Total Weight (Kg) |
| L | 12 | 2 | 2.95 | 5.9 | 0.89 | 5.251 |
| L1 | 12 | 4 | 2.07 | 8.28 | 0.89 | 7.369 |
| L2 | 12 | 4 | 2.01 | 8.04 | 0.89 | 7.155 |
| L3 | 12 | 4 | 1.91 | 7.64 | 0.89 | 6.799 |
| TOTAL | 26.57 Kg | |||||
Happy Learning 🙂
